En algún momento aburrido de nuestra vida, todos nos hemos puesto a dibujar patrones recursivos en la hoja de papel más cercana sin saber realmente lo que estábamos haciendo. Por ejemplo, una línea de la que salen dos líneas al final empieza a convertirse en algo agradable a la vista tras unas pocas repeticiones.
Este concepto tan simple es una figura fractal: un objeto geométrico autosimilar.
Espera, espera, ¿Qué es eso de autosimilar?
Es la manera bonita de decir «si haces zoom en un sector de la imagen, ésta seguirá pareciendo igual (o casi igual) que la original porque estás repitiendo el mismo patrón una y otra vez«. Dicho sin palabras:
La figura que acabamos de ver, en concreto, se llama árbol pitagórico, no porque Pitágoras tuviera algo que ver con su invención, sino porque su primera formulación fue construida usando cuadrados y su inventor, Albert E. Bosman, decidió bautizarlo con el nombre del rey de los cuadrados.
Otro diseño fractal consiste en dibujar triángulos en los lados de un triángulo y a su vez meter más triángulos en esos triángulos y repetir el proceso hasta obtener tantos triángulos tan pequeños que parecen una línea a simple vista y terminar aproximando una curva que… Que noo, que adjuntamos una animación de lo que hemos descrito, llamado la curva de Koch:
Crédito: wikimedia commons.
O, ya que hablamos de triángulos, os presentamos la pirámide de Sierpinksi:
Fuente: wikimedia commons.
Pero no nos conformemos con las líneas en blanco y negro.
Hay figuras fractales más complejas que representan conjuntos de números obtenidos mediante fórmulas matemáticas. Un ejemplo es el fractal de Mandelbrot, conseguido representando sobre este plano los números que pertenecen al conjunto de números que cumple:
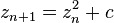
Lo que nos da un patrón bidimensional que, por mucho que aumentemos, seguirá poseyendo una geometría similar a la imagen original.
Los colores están añadidos por separado para poder distinguir algo.
Más interesante es el hecho de que estamos rodeados de formas fractales… Más o menos. Una figura fractal, por definición, contiene infinitas iteraciones de los mismos pasos, algo que es imposible en la vida real, fuera del plano matemático. De lo que estamos rodeados en realidad es de figuras que se asemejan a fractales, como los patrones que van erosionando los ríos a medida que fluyen…
Las marismas del parque de Doñana tienen cierto carácter fractal.
O la línea de costa, que por mucho que hagas zoom hacia ella, sigue compuesta por el mismo tipo de curvas cada vez más pequeñas… Hasta que llegas a algún pedazo de piedra o arena y deja de cumplirse la propiedad fractal. En el siguiente ejemplo, hemos usado la costa oeste de la isla de Ibiza.
Click en la imagen para ampliar.
Aún así, es muy interesante el hecho de que las formas fractales aproximadas también están presentes en los seres vivos porque tienen dos ventajas: son eficientes distribuyendo el espacio y son fáciles de codificar. Por ejemplo, almacenar la posición exacta de cada uno de nuestros vasos sanguíneos o nervios conllevaría una cantidad brutal de datos, así que nuestro ADN contiene instrucciones «fractales» que permiten minimizar la cantidad de información contenida en el código genético, ya que proporcionan unas directrices para su desarrollo en vez de describirlo componente por componente. En vez de decir «coloca esa vena allí, luego lleva otra allá y procura pasar esta por ahí también, luego…«, nuestro código genético ordena «tira esta vena y haz bifurcaciones a tal distancia hasta que te canses» (interpretación libre).
Distribución de las venas y arterias en el cuerpo al estilo «árbol Pitagórico». Fuente, aquí.
Lo mismo ocurre en el crecimiento de las ramas de los árboles (esta era bastante obvia) o en el broccoli romanesco, cuyas flores maximizan la cantidad de superficie expuesta al sol.
«¡Niño, cómete tus fractales o no hay postre!»
Sólo por si acaso, para terminar la entrada, queremos aclarar una cosa: las figuras fractales de ocurrencia natural no son la prueba de la intervención de ninguna inteligencia superior, ni tienen nada de espiritual. La naturaleza no es sabia, es vaga (sólo que mucho más eficiente siéndolo que nosotros).












3 comentarios
Interesante artículo, ahora que mencionas los fractals ¿verdad que había una fórmula para encontrar el área de estos?
Con una integral
Hola!. Me parecio muy interesante esta nota y me da un poco de nostalgia porque a mi me interesa este tema y me gustaria contarles que yo me hice un analisis de adn y asi pude conocer a mi padre.Gracias realmente. Saludos!!